学习Sinkhorn Distance后的个人理解
summary
本文简单介绍一下最优传输理论中的Sinkhorn Distance及其求解的方法，并提供了Python代码实现
type
Post
status
Published
slug
202305042300
category
Research Notes
date
‣
tags
Machine Learning
Python
icon
password
comment
SLUGS
由于网上各位大佬都做了足够多的介绍，我这里当个缝合怪，顺便说说自己的理解。若有疏漏，请斧正！
概念
什么是Sinkhorn Distance？它是一种optimal transport distance。
什么是optimal transport distances呢？我们不妨说说其中很常见的推土机距离。
什么又是推土机距离呢？那下面就做个简单的介绍。
推土机距离
Wikipedia的对推土机距离的解释是：
In computer science, the earth mover's distance (EMD) is a distance-like measure of dissimilarity between two frequency distributions, densities, or measures over a region D.
简单来说，推土机距离是衡量两个分布之间的距离的一种方法。它的基本思想是将一种分布通过一定的代价转换为另一种分布，计算这个代价就是推土机距离。
你可能了解过度量两个分布的其他距离，如欧氏距离、KL散度、JS散度以及其他更复杂的距离，但是这类距离方式并未考虑两个分布之间的联合分布。而推土机考虑了：
其中，是所有联合分布的集合，其边缘分布分别为。
求解这样的式子，得到联合分布，也就是最终的推土方案：
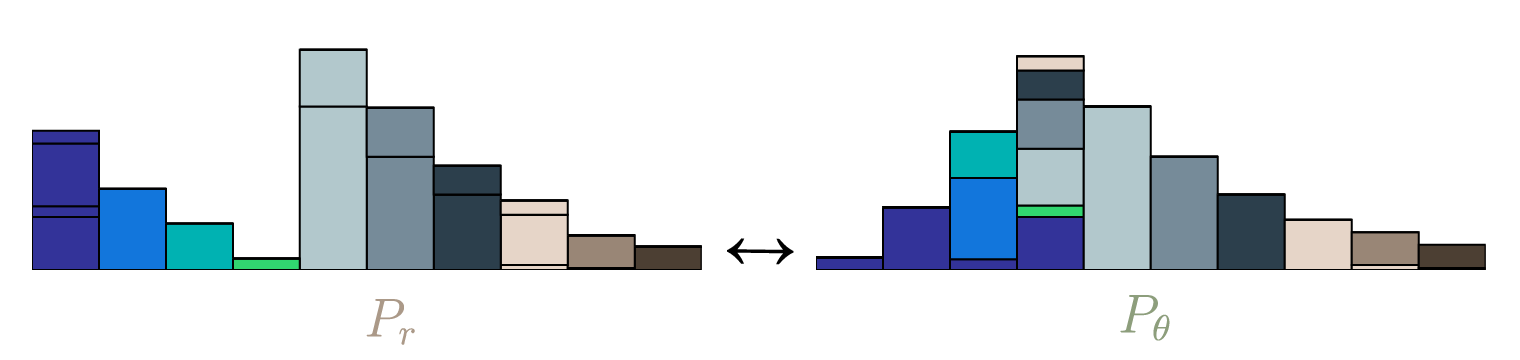
Optimal Transport Distances
介绍完推土机距离后，回到optimal transport distances上。
假设有这样的交通运输场景⁵：有个仓库，个工厂，我们需要将某种物品从各个仓库运送到各个工厂（允许一个仓库的物品运往多个工厂，且允许一个工厂接受多个仓库的运货），希望找到最优运输方案来最大限度地降低运输成本，这便是最优传输问题。
假设第个仓库存货量是，第个工厂的需求量是，仓库到工厂的运输距离是，表示从第个仓库运货到第个工厂的货物量，那么求解这样的问题其实是在求解如下的线性规划：
和推土机距离的联系：
（下面均假设，理论上可推广至的情形），仓库和工厂可看成两堆不同的土，各个仓库的存储量情况和各个工厂的需求量情况可以看作两个分布，各个仓库和各个工厂的距离可以看作为两个分布（直方图）各个区域间的距离。
上面通过求解(2)式获得的就是最优传输距离，下文称之为原始optimal transport distance。
然而一些工作在(2)式的基础上加了一些约束，使其便于求解，因此就有了不同“版本”的距离，统称为optimal transport distances。例如常见的有：
- Wasserstein Distance (也称推土机距离)：用于WGAN中，使用Lipschitz正则化(1)式的对偶形式中引入的函数。不过一些人认为WGAN中计算的分布间的距离并不是严格意义上的Wasserstein Distance。
- Sinkhorn Distance: 它是Wasserstein distance的一个近似算法，使用了熵正则化的方法实现计算上的效率。通过引入熵惩罚项，可以将概率分布之间的optimal transport问题转变为具备良好计算性质的解析表达式。
- Cramer Distance: 一种用于测量两个概率分布之间距离的方法，它是基于分布函数的平方差来定义的。Cramer Distance的提出是为了解决Wasserstein Distance在梯度计算中存在偏差的问题。
而今天本文的主角是“Sinkhorn Distance”，下面开始介绍。
Sinkhorn Distance
为什么文献[1]会提出Sinkhorn Distance呢？
其主要针对原始optimal transport distance的时间复杂度高这一问题，提出了一种最大化熵的约束方案来使传输方案不那么稀疏，并且降低了计算复杂度。具体而言，原始optimal transport distance存在的缺陷：
- 计算复杂度高：在针对两个d维的直方图的optimal transport distance时，至少需要。当测度空间嵌入到，在高维直方图上计算该距离的成本是非常巨大的。
- 稀疏性：由于计算原始optimal transport distance的是在求解线性规划问题，因此最优解通常出现在可行域的顶点处，落在顶点处的解通常是比较稀疏的。例如对于两个维直方图，使用线性规划求解的传输方案为的稀疏矩阵，且最多有个非零元素，从概率角度看，如果，具有很少的能使得。即一个仓库偏向于只为少量（甚至一个）仓库供货。这样的稀疏可能并不符合实际场景，以至于计算得到的并非最优解。
Sinkhorn Distance便是针对这两个问题提出的一种lightspeed computation、sufficient smoothness的optimal transport distance。
回顾optimal transport distance
这里对上面提到的原始optimal transport distance做一个形式化描述：
对于在单纯形中的两个概率向量和，记到的所有传输方案集合为：
表示全1的列向量，包含了行和列总和分别为和的所有非负矩阵。对于取值均在的两个多项随机变量和，每个变量分别具有分布和，包含了所有关于的联合分布。对于，有。
那么对于和间的optimal transport distance定义为：
其中代表Frobenius dot-product（矩阵对应元素相乘的和，相当于对Hadamard product的结果求和）。在有些论文中，上述的表示可能是：
最大化熵
Sinkhorn Distance提出将(4)中的进行smoothing，在机器学习领域很容易想到的就是最大化熵，即最大化，下面先探讨一下的上界。
符号说明：
由[7]中的公式知：
因为是和的联合分布，那么根据(6)有：
因此的上界是。显然h(P)不能严格靠近其上界（会导致过度平滑），且与上界的距离不应超过一定阈值（否则会过度稀疏），即：
且易证：， ，
因此有：
用(9)来约束得到：
其实直观上看，这个约束就是将运输方案和拉近。（那么这个到底是什么呢？见补充部分。）
定义
根据上述，可以得到Sinkhorn Distance的定义：
一般有了定义，会探讨有哪些性质，这里就不展开了，有兴趣的可阅读文献[1]。
简单来说，在不是特别小或者特别大时，满足对称性和三角不等式。
对偶形式
直接求解(11)式是比较棘手的，可以考虑(11)式的对偶形式：
对(11)中的每个，都能在(12)中找到合适的使得
成立。如此便将较复杂的约束转换为惩罚项。这里的被文献[1]作者称为dual-Sinkhorn divergence。
这里文献[1]作者给了一个描述原始optimal transport distance 、Sinkhorn distance 以及dual-Sinkhorn divergence 之间关系的示意图：
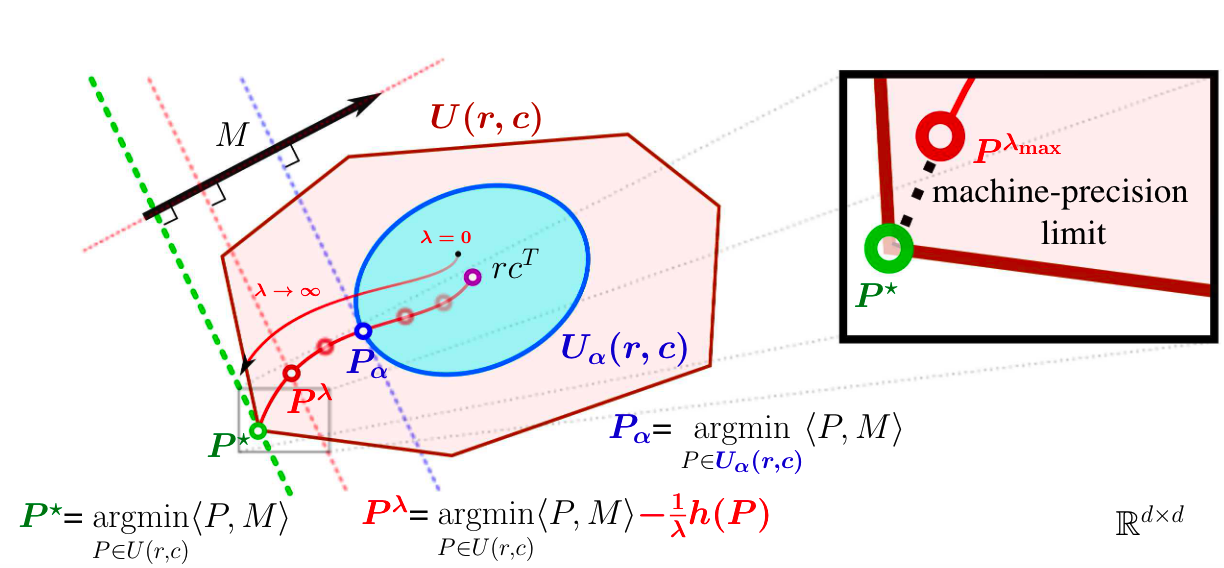
由上图看出，可以从0逐渐增大，来找到满足的。然而在实际使用中，这样去找是不切实际的（会带来很多计算量），因此通常靠先验来选择可能合适的。
⚠️从公式(12)中可以看出，（求解公式(12)的过程中）的熵随着（预定义的）的增大在递减。也就是说，如果选了太大的会导致公式(12)得到的的熵偏低，因此不宜太大。
使用Sinkhorn’s theorem求解
得到(12)形式的dual-Sinkhorn divergence后，使用拉格朗日乘子法，可以得到：
其中是两个等式约束的系数。对求导并令，得：
注：这里文献[1]作者可能是将对数的底数当作来进行处理的。
根据(14)可知应该有这样的形式:
其中，中是待求的两个向量。
根据文献[8]所提出的Sinkhorn’s theorem可知：中有且仅有唯一的能表示成的矩阵，并且可以通过Sinkhorn’s fixed point iteration来求解：
文献[1]作者给出了Matlab风格的伪代码：
原文还给了其他有趣的证明和说明，有兴趣的可以阅读原文。这里就暂不往后阐述了。
Python代码
在参考大佬们的Sinkhorn distance实现后，为了接近原文伪代码，我稍做了修改后的Python代码：
完整demo见zfhxi/Sinkhorn-Distance-Python。
下面是该demo的可视化结果：
上图可以看出是相当光滑的。
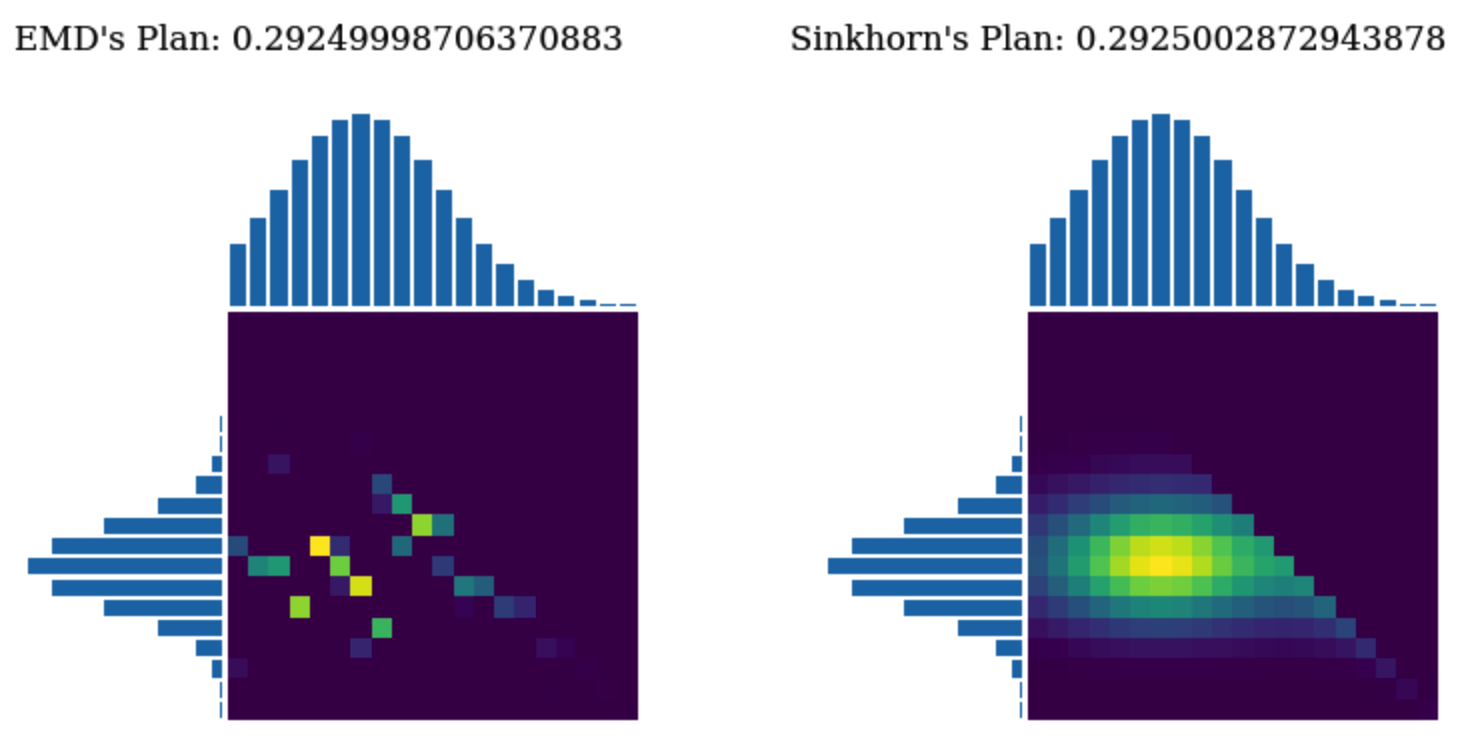
上图可以看出相比于线性规划求解的运输方案，Sinkhorn distance得到的运输方案更加平滑。
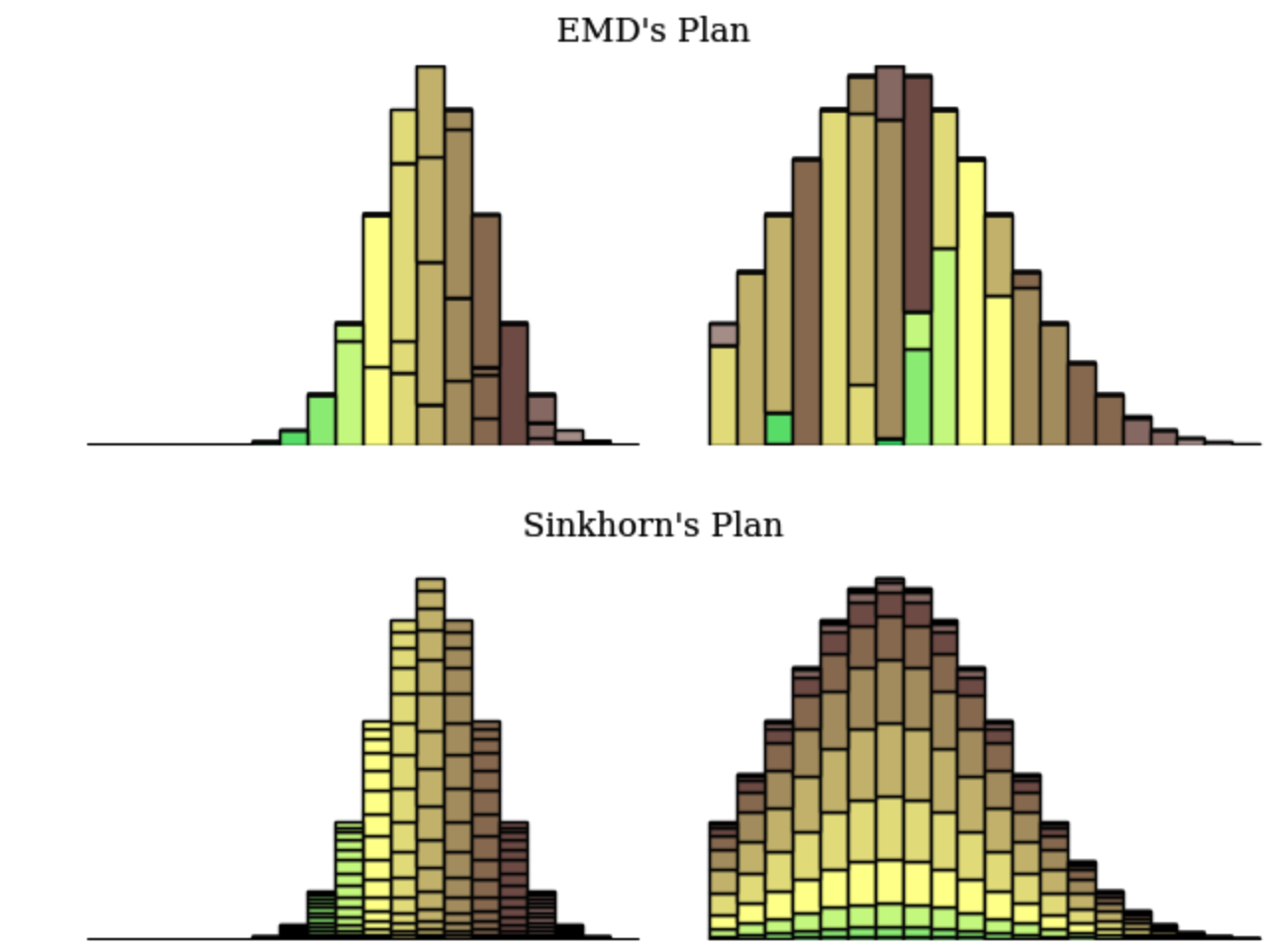
上图可以看到，Sinkhorn将直方图切分成更多的块，那么对应到实际场景，可能带来的问题是：运输货物时需要更多的车辆，或者说需要运输多次……
补充
KL散度、JS散度、EMD距离的优缺点
- KL散度不具备对称性且不满足三角不等式，仅考虑边缘分布；
- JS散度具备对称性，但在两个分布距离较远（比如均值差异大）时，变成一个常数，且仅考虑边缘分布；
- EMD对称且两个分布距离较远时仍能有效衡量距离，考虑了联合分布，但其计算复杂度比上面两个距离都要高出很多。
代表什么
根据文章[2]的解释并结合上面提到过的例子，意味着：
- 只有中数值比较高（较低）的索引和中数值较高（较低）的索引相乘后才能使得更高（更低）；
- 并且中数值比较高的索引和中数值较低的索引相乘后并不能使得更高。
也就是说：
- 对于一些仓库来说，如果它存储量更多，就应该运出更多货物；对于工厂来说，如果它需要更多，就应该从每个仓库那里按比例获得更多。
- 对于货物存储量很多的仓库，它不会主要向需求量少的工厂运输货物。
代表了一种十分光滑的运输方案，见demo中的可视化图。
不动点迭代法
什么是不动点迭代法参考：不动点迭代法—单变量非线性方程近似根matlab求解 - 知乎 (zhihu.com)
相关待读
参考
Loading...