[论文简读][NIPS20]Generalized Focal Loss: Learning Qualified and Distributed Bounding Boxes for Dense Object Detection
summary
type
status
slug
category
date
tags
icon
password
comment
SLUGS
第一次读NIPS的论文,果然感觉有点费力啊,有些东西还是看得不够深刻,理解力不够,姑且写个笔记记录下吧。
另外,看完论文就写笔记这种读论文的方式,我已经坚持不下去了。问了学长,他说他坚持没到一周就放弃了,后面读论文就很自然了。所以我也开始自然一点吧。
Motivation
现有工作的两个问题:
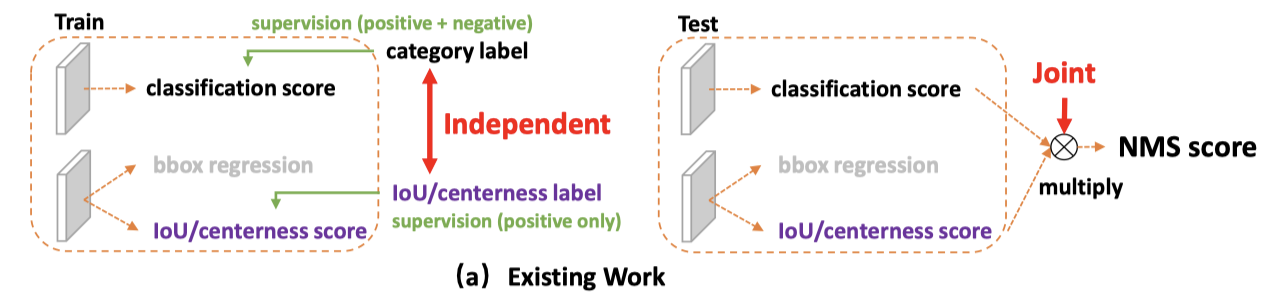
- 测试阶段的(检测)质量评估和分类流程,与训练阶段不一致。体现在( 见下图(a) ):
- 检测和分类分数在训练阶段是分别、独立地得到的,而在测试阶段,又把两者组合用来评估最终结果。
- 只对正样本分配定位监督信息,然而负样本也可能不可控地具有高的IoU score。

- bbox表示值的分布,通常用Dirac delta distribution来估计,不灵活。
- 通常把对bbox的预测值先验地认为服从Dirac delta distribution或者Gaussian distribution,然而实际的分布可能更加随意、灵活。
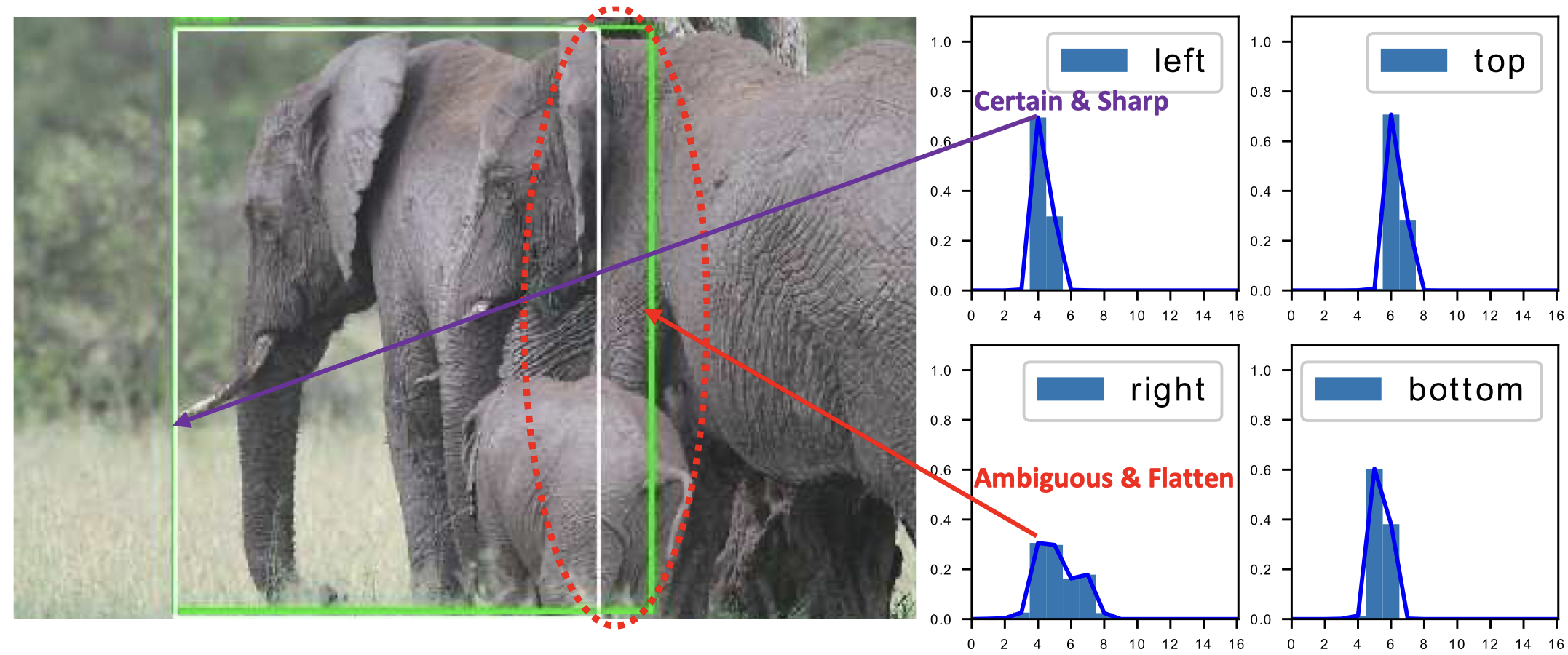
- 比如下图的大象,右边界由于遮挡其实是模糊不清的。强行用Dirac delta distribution来建模来回归到确定的预测值,可能会损害模型定位性能。
针对问题所提出的解决方案:
- 针对问题1,作者的想法很简单,整合classification score和IoU score,统一成一个表示(作者称为“classification-IoU joint representation”)。
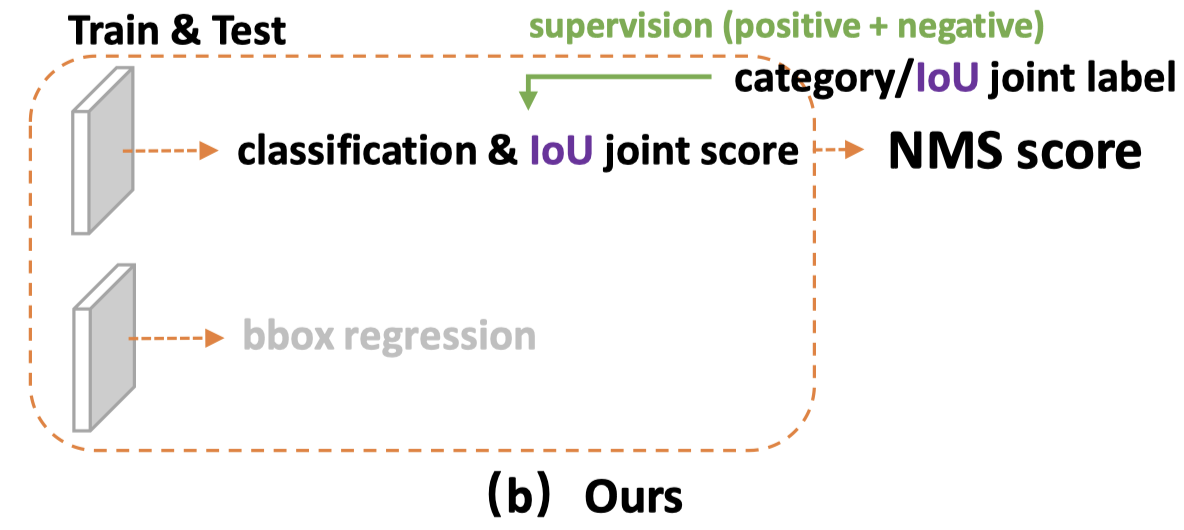
通俗解释就是,classification score的监督信息不是一个one-hot吗,作者把one-hot中的1改为IoU score(将one-hot soften),从而使两者关联起来。我个人理解,这样就算你负样本IoU score高,但classification score低了,模型会促使IoU score低下来。
- 针对问题2,作者称其不引入任何强先验条件下,直接在连续空间上学习离散化的概率分布来建模bbox representation的分布(抛弃了强先验的Dirac delta distribution和Gaussian distribution)。也就是说,作者希望那样:针对确定的边界,其分布类似Dirac delta distribution那样尖锐;而针对模糊的边界,其分布可以相对平一点,如下图。
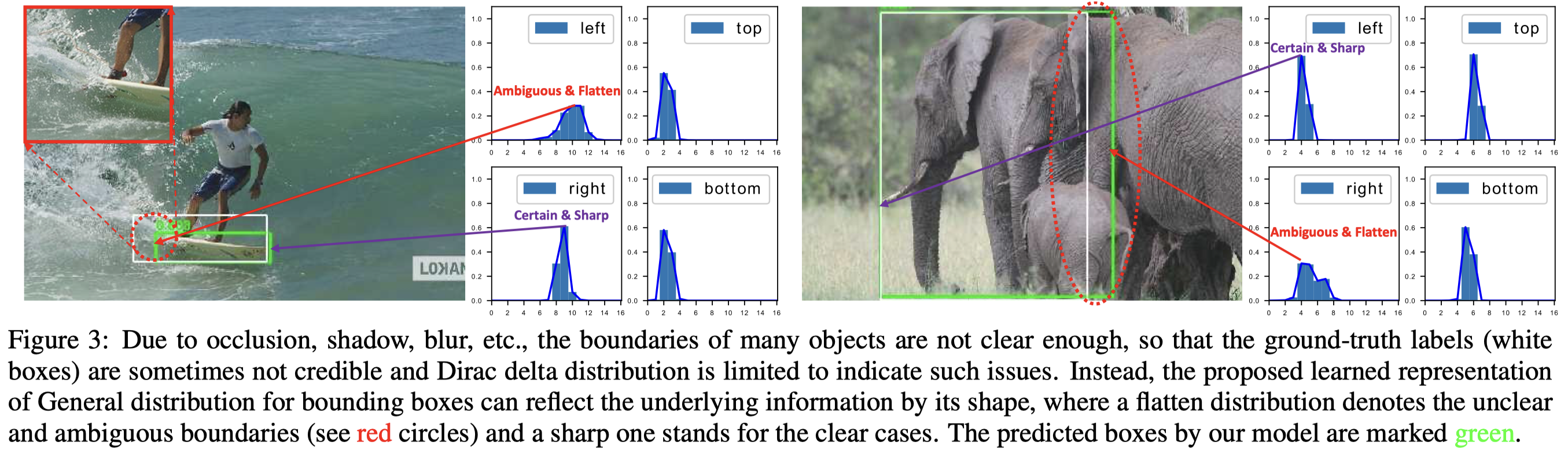
具体地做法:作者使用bbox表示的gt值的附近离散值,配上了权重,这样就可以得到“arbitrary distribution”(积分后得到的值就是gt值),用这个分布作为bbox representation预测值分布的target。
Core Method
作者在Related Work部分简短地描述了存在这两种不足的相关工作,就不细述了。直接上方法部分。
目标检测中的Focal Loss(下文简称FL)一般仅支持这种离散的label类别。前述的classification-IoU joint representation里的label是0~1的连续值。因此作者在FL基础上做改进,提出Generalized Focal Loss(GFL)。
- 首先回顾FL:
其中,分别代表类别gt值和预测值。是可调节的focusing参数。具体地,FL其实可以看成标准的交叉熵项和一个动态放缩项组成。后者随着训练过程会逐渐降低简单样本的损失贡献,从而关注难样本。
- 为了解决训练和测试的不一致性问题(即前述的问题1),如前面提到的,作者将one-hot进行soften。但是FL仅支持离散的label,于是作者改进,提出了Quality Focal Loss(QFL):将替换为;并且将替换为。
其中表示对各个类别上的IoU score预测的Sigmoid值,表示真实的IoU score,表示真实与预测值之间的差距绝对值,实验中最终选择了2。最终组合形成了QFL:
当IoU score估计得不准确时,会很大,那么损失贡献就会提高,模型就更关注难样本的学习。
- 为了解决bbox representation预测值分布建模问题,作者提出了Distribution Focal Loss(DFL)。
- 首先回顾Dirac delta distribution怎么建模的:因为bbox的表示通常是通过positive points加上w,h或采用(left、top、right、bottom)来表示的。通常希望预测值能回归到真实距离值,因此按照Dirac delta distribution建模的结果是:
- 根据前述,作者尝试用任意离散分布来建模,对于给定的的范围,那么预测值也应,从而有:
- 进一步化简。能得到的分布太多了,比如说:
- 个人理解。从公式上看,的误差范围(可模拟的模糊取值范围)是,而且最终作者的实验中。似乎的变化范围也不大,那么最终分布也会很sharp。然而,如果这个呢?那么的变化范围应该是,对于模糊的边界,容错范围变大了。
- 简单欣赏下作者怎么实现DFL这个损失的:
那么为了得到预测值,只需要积分即可:
为了可以计算,作者又将范围按照间隔离散化到,。最后的实验中,作者将设置为1。因此,预测值可表示为:
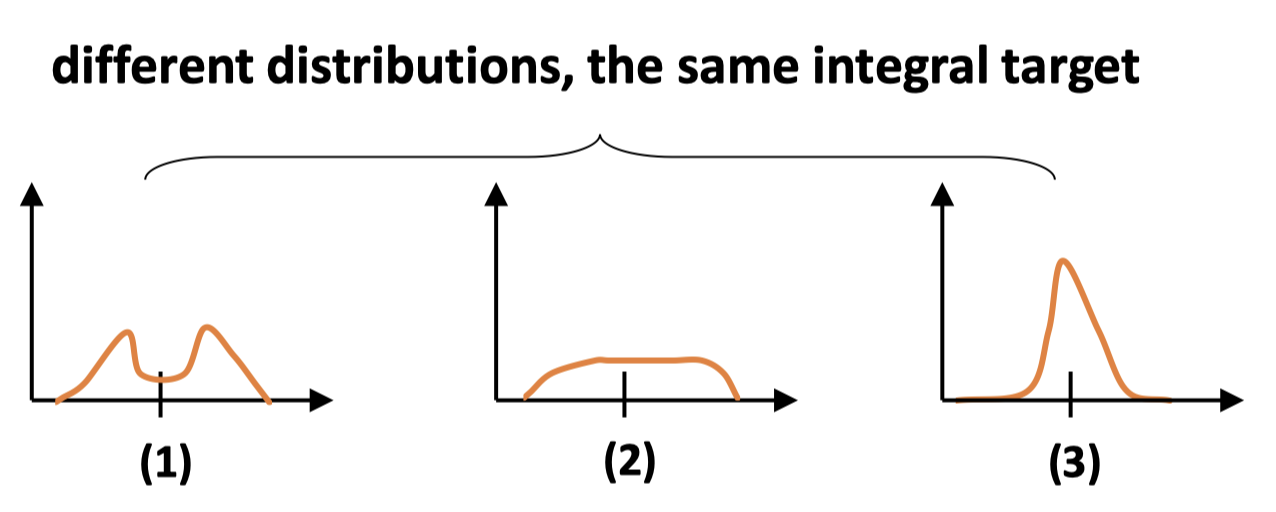
显然(3)才是比较合理的。因此作者希望靠近附近的的概率高,于是简单地只考虑了的概率,其中。由于bbox的学习只针对正样本,不存在类别平衡问题,作者简单地使用了标准交叉熵来构建DFL损失:
其中,那么预测值其实可以表示为:
- 原文中,作者把QFL和DFL统一到一个形式,形成了Generalized Focal Loss(这里我只想扔个截图,因为个人觉得这是作者为了形式上的好看、方便将两者统称为GFL,所做的一些说明):

- 最后的损失:
其中分别代表QFL、DFL、GIoU Loss
后面的实验部分,我只扫了一眼,就直接略过。
Personal Reflection
- 将IoU score融合到classification score中,从而解决训练和测试不一致问题,很有新意。
- 另外,对边界分布构建通用的离散分布来估计,增加一定容错能力,这个角度挺有创新性的。
- 作者在使用FL中,似乎移除了系数,虽然作者文中是说为了表示的简单。但最终他似乎也未使用该系数来平衡正负样本平衡,这是我现在疑惑的一点。
Loading...