初学VAE【01】概念到推导
summary
type
status
slug
category
date
tags
icon
password
comment
SLUGS
本文笔记主要来自文献[1]。
小提生成模型
在说VAE(Variational Autoencoder)之前不得不先说生成模型(Generative modeling)。生成模型是对数据样本(datapoints)在高维空间上定义了其分布的模型。这样在潜在空间取一个点(隐变量值),就可以得到这个点生成的高维空间上的样本(新样本)的概率。图像生成应用中,可以判定生成模型生成的图像是不是合理的,然而知道生成的图像合不合理,并不能始终都能生成一个合理的图像。
这类生成模型的本质是:数据样本的分布通常是一个未知分布,目标是去建模一个分布,使得分布与尽可能接近(即样本对应的隐变量值,又去生成一个样本,使与的距离相近,这样可以通过生成的数据来推测原数据样本的分布)。
这类方法通常可能会有的缺陷:
- 需要对数据样本的结构进行很强的假设。
- 进行了严格的近似,导致性能次优。
- 推理过程计算耗时,比如Markov Chain Mente Carlo采样。
所幸神经网络已经很成熟,可提供给力的函数近似器来构建生成模型。最主流的便是Variational Autoencoder。
再论隐变量模型
隐变量模型的核心是隐变量这一概念,什么是隐变量呢?举个手写数字数据集MNIST的例子。在生成数字之前,模型首先需要从中采样数值,再通过保证图像的轨迹要匹配来生成图像,其中就是隐变量,它隐式表达了图像包含的数值信息。
对隐变量模型而言,对每个样本,从定义在高维空间上的概率密度函数中采样,至少有一个,可通过由向量参数化的确定函数族来生成样本,且生成的与极其相近。其中。
对于数据集中的每一个样本,我们希望最大化以下概率(似然函数):
其中分布是对的替换。在VAE中,通常有,其中是超参数。这种替换的初衷是,在训练早期,模型不会产生与相近的输出,由于其为高斯分布,通过慢慢优化,可以让中采样的某些下的靠近,而采样的其他下的与也相似。
注意:
- 模型早期的输出与相距较远,所以较低,式(1)的积分通常通过采样求得,因此其近似依赖于的大小),就代表着不好,通过训练,去找好的,那么采样的周围的可生成相似样本。
- 如果是狄拉克函数(近似于没做替换),训练早期与相距远,而是由(此时也近似服从狄拉克分布)生成的结果,同样通过训练找到了好的,然而周围的不一定能生成相似样本(甚至可能不是合理的样本)。
(这里还是有点乱,后面再捋一捋,原文似乎想暗示,从这个“替换”就可以感受出VAE和自编码器的一点区别。)
后言变分自编码器
VAE就是最大化式(1)似然率,针对式(1)的积分形式,可以引出VAE的两个核心问题:
- 如何定义隐变量,其代表什么信息?
- 如何沿进行积分得到似然率?(因为被积项中的通常没有严格的解析表达式,而且被积函数可能复杂,其积分不一定有解析解)
定义隐变量
对进行定义的过程中,一般注意如下先验规则:
- 避免显式定义的每一维代表哪些信息。
- 避免显式描述各维度之间的依赖(即的结构)。
因此VAE对的假设如下:
- 的每个维度的信息难以简单的理解。
- 所有数据样本生成的隐变量们可以简单假设都服从正太分布。即。
对于第二点,基于任何维分布都可由服从高斯分布的维随机向量经过复杂函数映射得到(下图是一个简单示例)。
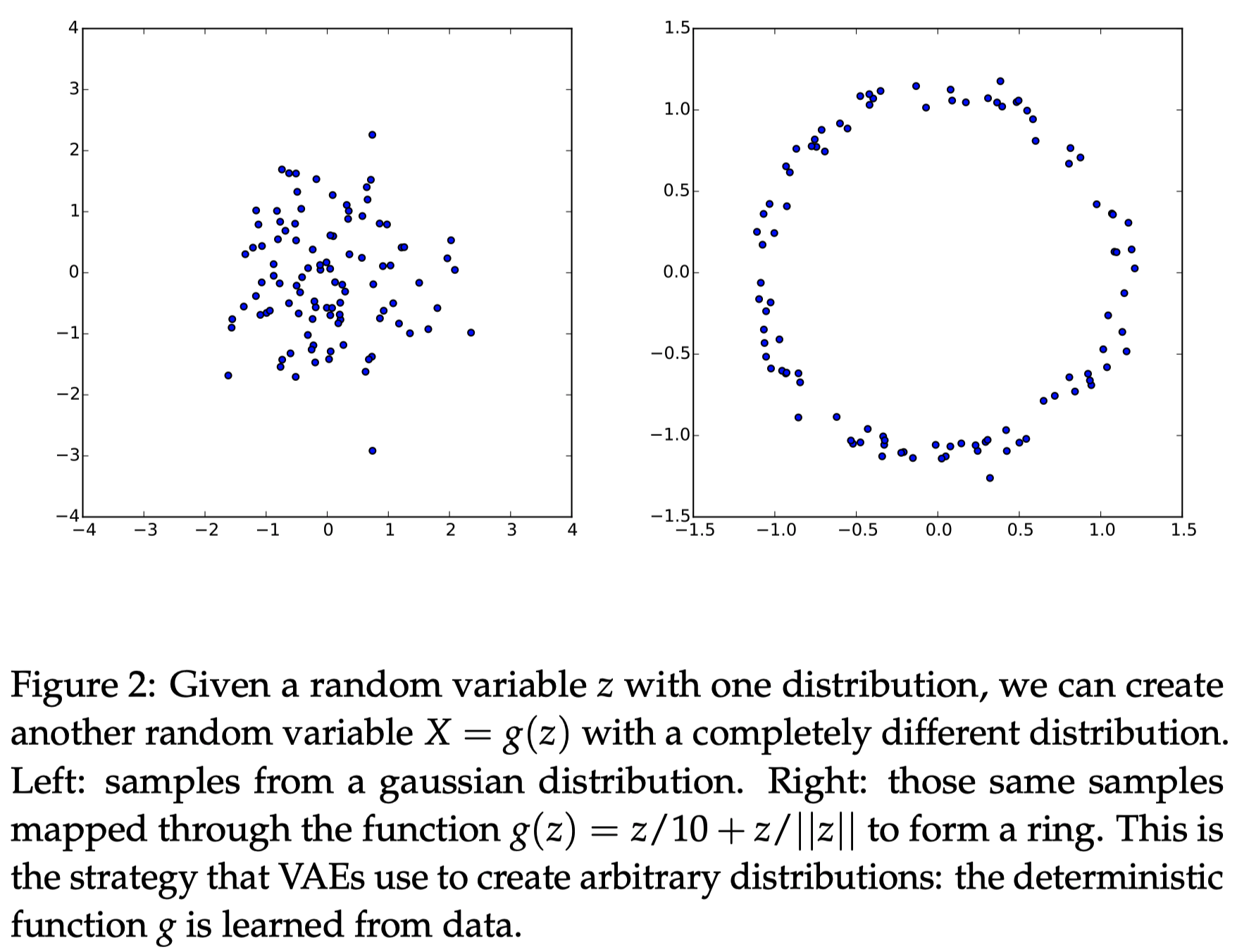
因此可通过学习强大函数近似器,来将各维独立同分布的随机向量映射成模型需要的潜在变量,然后通过这些潜在变量再映射到生成样本。
回顾下式:
如果是多层神经网络,它的前几层将映射到真正的“隐变量”(比如手写数字的值、轮廓等)
,接下来的几层将真正的“隐变量”映射成生成样本。一般而言,我们不用关心隐变量的潜在结构(各维代表了什么信息),如果隐变量能使得精确生成训练集,那么在网络的某一层学习到了隐变量的潜在结构。
求似然率过程的思考
解决隐变量定义问题后,接下来面临的问题就是如何最大化式(1)的似然率了。
如果被积项中有解析表达式(式(3)中为表达的简洁,省略了),那么可以基于梯度的方法来优化得到最大似然率,然而往往很难得到解析表达式。另外,从概念上而言,计算是比较简单的,通过采样大量的然后计算:
,这样计算也是可以的,并且也可继续使用基于梯度的方法来优化。
引入分布对重要的进行建模
然而式(3)中有一个问题,当样本维度很高时,为了精准近似那么就得相当大,计算效率很低。但实际中发现,虽然会很大,但大部分的偏向于0,因此对的近似几乎没有贡献。此时,VAE考虑引入一个新分布,其表示了能重新生成样本的关于值的分布,而这个分布通常不是标准高斯分布(可能是高斯的,但不是均值为0,方差为单位阵的高斯分布)。怎么通过这个分布来优化呢?
考虑和的关系
首先对分布(它可能依赖或者不依赖)与后验之间的Kullback-Leibler divergence:
对式(7)进行移项:
式(8)便是VAE的核心(一些文献有如下定义:表示关于数据集本身的信息,称之为
Evidence,右侧称之为Evidence Lower Bound (ELBO)。而最大化Evidence,就是最大化右侧的ELBO)。由于我们感兴趣于推断,因此构建依赖于的是有意义的,尤其是使得更小的话,因此直接用来替换以仅保留和有关的的值的分布:这样就可以用分布近似难求的后验分布,进而中采样的就能较精确的生成。并注意式(9)右边,是可以通过基于梯度的方法来优化的,并且形式很像一个自编码器,将编码为,将其又解码为。
如何优化目标
如何对式(9)的左侧进行优化呢?其实是相当于优化右侧。
首先要确定的形式,通常的选择是,其中和都是由参数(可通过数据样本来学习该参数)控制的确定函数。通常在实现过程,确定函数往往选择为神经网络,并且被约束为对角阵,以便计算。
右侧第二项
先处理第二项。按照前面对形式的预先假设,那么右侧第二项的散度可以表示为两个高斯分布的KL散度,可得到闭式解:
其中是分布的维度。且VAE假定可以服从一个简单的标准高斯分布,因此代入式(10)得:
可从这个闭式解来求得梯度进行更新这一项。
右侧第一项
对于第一项,可以通过采样方式来计算,但是要精确估计需要采样很多,计算代价变大。所以VAE考虑如何选择少量的来估计期望。然而,VAE甚至只选择一个来计算期望,原因是,这符合stochastic gradient descent(随机梯度下降)策略的标准(如果忘记了SGD和BGD的区别,见《批量梯度下降和随机梯度下降的区别》),而且足够次迭代后,不同的都会被采样到。另外该文章《变分自编码器(三):这样做为什么能成?》从实验结果来说明后验分布是一个方差很小的正态分布,那么多次采样的几乎和均值相近,和一次采用几乎没多大区别了。
那我们可以对数据集中所有样本进行SGD,需要优化的完整式子如下:
如果我们对式(12)进行梯度计算,那么梯度符号可以放入期望的每一项中(类似操作)。因此,每个step,都需要从中采样一个和,来计算下式的梯度:
然后我们又可以对任意多的这种采样计算得到的梯度进行平均,这样可收敛于式(12)的梯度。
注意到,不仅依赖于的参数,还依赖于的参数。然而在式(13)中的第一项并未显式表达对的依赖,这只是一种表示上的失误。从另一种方式来理解的话,可见下图左部分:
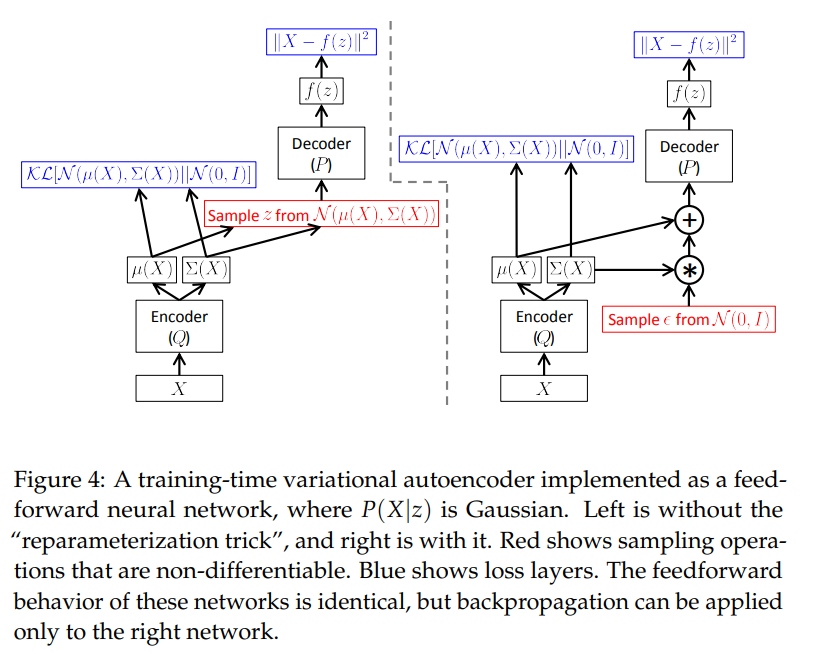
Re-parameterization trick
另外,采样是一种不连续的操作,无法对采样操作得到的结果计算梯度。如上图左部分,如何将采样的和的结果关联起来以计算梯度呢?针对此,VAE采用了"reparameterization trick",如上图右部分:对输出的均值和方差,我们从进行采样时,可先采样,然后通过来得到采样结果。因此,实际上是基于下式的梯度在进行优化:
值得指出的是,"reparameterization trick"工作的条件是:
- 采样可以通过一个评估一个噪声的函数来确定,指噪声值(上式指)。
- 关于的映射应该连续,这样才能反向传播(这里指、应该连续)。
显然,上述采样的满足条件(为噪声值,为与、和相关的函数)。
测试阶段
其测试阶段如下图:
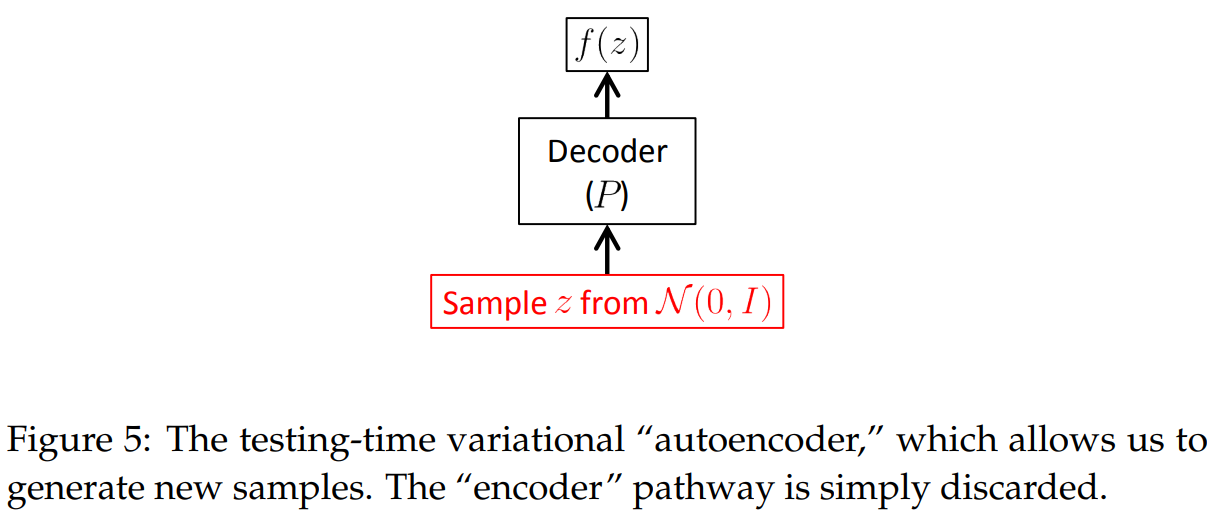
移除了编码器,直接从中采样作为的值,输入到解码器中生成样本。
另外注意到式(9)
左边这一项始终非负,因此式(9)优化目标有一个下界,然而仍难以计算,需要通过采样来近似求解。在测试阶段,直接从中采样来近似要比又使用"reparameterization trick"高效,因为不需要求梯度了。这样求得的下界粗略反映了模型捕获数据样本的信息量。
参考
Loading...